|
|
| |
SHUNTING PUZZLES
|
| |
|
| |
| SHUNTING, as
defined by the Oxford English Dictionary,
primarily describes the act of "pushing or pulling a train or part
of a train from the main line to a siding or from one
line of rails to another: their train had been shunted
into a siding". While this
conforms to British and Australian usage, its equivalent
in North American railway terminology as used by the US
Department of Transportation is SWITCHING.
|
| |

John
Vaughan photograph, (c) Adrian Wymann collection
|
|
Commonly, this is done by
purpose-built shunting locomotives, but in remote
or less frequently visited locations, shunting
duties are performed by the same locomotive used
to haul the train on the mainline. Such is the scene at the
Parkandillack china clay works in Cornwall in
February 1982, where Class 37 135 (a Co-Co
locomotive weighing no less than 102 tons) is
shunting its train, while illustrating at the
same time that shunting almost always involves a
lot of legwork by railway staff.
|
|
| |
| Evidently, the terms shunting
and switching denote the same procedure and are
completely interchangeable; the heading of this page,
SHUNTING
PUZZLES, can
therefore also be read as SWITCHING
PUZZLES. |
| |
| |
My favourite definition
of PUZZLE
actually has a few layers of dust to it, as it
comes from the 1911 edition of the Encyclopedia
Britannica. However, as puzzles aren't new,
it still captures the essence in a miraculously
short sentence:
"PUZZLE: a perplexing question,
particularly a mechanical toy or other device
involving some constructional problem, to be
solved by the exercise of patience or
ingenuity."
Clearly,
this is something real railways and railroads
would like to keep to a minimum in daily
operations. The two concepts are only brought
together voluntarily in the field of railway
modelling (model
railroading) where shunting puzzles
can generally be described as being reasonably
compact layouts which - by way of definition
through their name - have two basic
characteristics:
|
|
 |
|
| |
| 1 |
|
First
of all, they are concerned with shunting, meaning
that they are conceived and built to allow
rolling stock to be moved around on an
appropriate track layout with sidings. On its
own, this is simply the definition of a shunting
layout. |
| |
|
|
|
| 2 |
|
Secondly,
this shunting is not done according to
spontaneous decisions of the operator but rather
follows a framework of set rules which create a
shunting order (usually by random selection of
both the cars to be shunted and where they are to
go), i.e. the operator is told what to do. This
deliberately introduces a range of more or less
complex and therefore difficult initial
constellations of the rolling stock which is to
be shunted, and thus creates the challenge of
successfully tackling the given shunting order.
It is this second aspect which is the key element
in turning a shunting layout into a shunting
puzzle. |
|
| |
A third characteristic, although
arguably a matter of taste, is that shunting puzzles
provide the most fun and sustained interest in operating
per square inch of model railway layout ...
|
| |

Shunting in
progress in the sidings at Little Bazeley, a 00 scale UK shunting puzzle
based on Inglenook Sidings
|
| |
It will
probably never be possible to determine where and when a
railway modeller first had the idea to turn a shunting
layout into a shunting puzzle. Most certainly, it was
someone who was looking for ways to make operating the
layout more fun, and probably also someone who liked
playing games. The first example I know of is Alan
Wright's way of operating his Wright Lines layout
in the 1950s, ultimately leading up to his classic Inglenook
Sidings, but there are bound to be earlier
instances. The other "classic" switching puzzle
is the Timesaver, devised by famed US modeller
John Allen in the early 1970s.
The
aim and purpose of this website is to illustrate and
explain how different shunting puzzles work and how best
to build and operate them. Over the years - not the least
thanks to the rise of the internet - many variations and
new types of model railway shunting puzzles have been
conceived and successfully built and operated by a
growing number of increasingly enthusiastic modellers.
However, no matter if you are a complete newcomer to the
subject or a seasoned shunting puzzler, it is always a
good idea to look to the two classic shunting puzzles for
information and inspiration.
All model railway
shunting puzzles generally belong to one of two different
types of puzzles: sequential movement
(where a pre-determined order needs to be formed) and distributional
ordering (where items must be placed where
they belong).
|
| |

DISTRIBUTIONAL
ORDERING
SHUNTING PUZZLE
Solving a distributional ordering
puzzle requires you to distribute individual
elements of a puzzle in such a way that they end
up being in what has been pre-determined as their
correct place.
BEST
KNOWN EXAMPLE:
JOHN
ALLEN'S
TIMESAVER

The
classic and by far the best known shunting
puzzle: John Allen's Timesaver, which was originally presented in the
November 1972 issue of Model Railroader.

|
|

SEQUENTIAL
MOVEMENT
SHUNTING PUZZLE
Solving a sequential movement
puzzle requires you to follow a series of
sequential movements within a set of strict rules
in order to arrive at a predetermined result.
BEST
KNOWN EXAMPLE:
ALAN
WRIGHT'S
INGLENOOK SIDINGS

The
classic British shunting puzzle is Alan Wright's Inglenook Sidings, which originated in 1978 but dates back
to a scheme already used by Alan Wright on his
1950s layout Wright Lines.

|
|
| |
|
| |
SHUNTING PUZZLES ON THE
REAL RAILWAYS?
|
| |
| Are shunting puzzles an aspect of
actual real-world railway operations, or are they
something only to be found in the imaginary world of
model railways? Railway companies
try to run their services as smoothly and as efficiently
as possible, and simple track layouts are one way of
achieving this.
|
| |

John
Vaughan photograph, (c) Adrian Wymann collection
|
|
Model railway shunting puzzles,
on the other hand, deliberately set up
complications, and it is in this approach that
the two worlds of real and model trains differ. However, there are many
locations served by real railways that can
provide quite a bit of head scratching for the
shunting crew. In those cases, the only
difference then lies with the terminology used;
in the real world, it is called a challenge and
not a puzzle, since it's not done for the purpose
of entertainment.
The scene at the
Parkandillack china clay works in Cornwall in
February 1982 illustrates this nicely - in order
to get the required shunting moves done, the
class 37 locomotive even has to sandwich itself
in between two rows of rolling stock.
|
|
| |
| Shunting puzzles thus do indeed
reflect at least some aspects of the reality of actual
railway operations. The chance distribution of rolling
stock (as opposed to logistical requirements dictating
where freight stock goes) could be viewed as artifical,
but then again, as the saying amongst railway modellers
goes, there's a prototype for everything. |
| |
|
| |
A LITTLE BIT OF
SHUNTING PUZZLE THEORY
|
|
| |
| Model
railway shunting puzzles are fun because they give a
sense to running trains by posing a challenge, and
finding the solution to this challenge is both satisfying
and entertaining. In this respect, shunting puzzles are
like any other puzzle. Therefore, in order to take a
"look behind the scene" and see how shunting
puzzles work, it is best to start with the general
question: |
| |
What exactly is a puzzle?
Puzzles come in many forms and styles,
such as riddles, mazes, jigsaws, blocks, rings,
wires, and lots more.
Some of the
oldest "mechanical" puzzles come from
China (perhaps the most familiar being the ch'i
ch'iao t'u or Tangram), while
possibly the best known historic European puzzle
goes back to a tale from Ancient Greece, dating
from 600 BC, and related by Sophocles and
Apollodorus: The famous riddle of the Sphinx
which sat on Mount Phikion
and asked the Thebans "What has one voice,
and is four-footed, two-footed and
three-footed?" Unless travellers gavethe
correct answer (which was "man" - crawling in
his infancy, walking in his prime and using a
stick in old age) they would be killed by the
terrible Sphinx...
The origins of
the word “puzzle“ itself are disputed.
It has been suggested that the verb to puzzle,
which appears at the end of the 16th century, is
derived from the noun apposal (meaning
"opposition"), indicating "a
question for solution".
Others assume
that the noun is in fact derived from the verb,
which, in its earliest examples, means "to
put in embarrassing material circumstances, to
bewilder, to perplex". Some connection may
also be found with a much earlier adjective poselet,
meaning "confused, bewildered", which
ceased to be used by the end of the 14th century.
|
|
 
|
|
| |
| |
Sequential
movement puzzle + trains = "the shunting
puzzle"
|
|
| |
| Jerry Slocum & Jack
Botermans, who are the authors of a scientific study of
the history and principles of puzzle games (Puzzles Old
and New, University of Washington Press, 1992), provide
an in-depth look at sequential movement puzzles. Sequential movement puzzles are related
to the well-known solitaire or peg puzzles, as well as
the famous Rubick cube. The solution to this type of
puzzle requires a user to follow a series of sequential
movements within a set of strict rules in order to arrive
at a predetermined result. Many puzzles of this type
first appeared during the 18th and 19th century in
Europe, often devised by mathematicians because they
involve certain principles of topology, number theory,
and combinatorics. However, as most of these puzzles are
intended to be fun, they can actually be solved with a
very basic mathematical knowledge - very often, logic and
trial-and-error are quite sufficient.
One very famous such
"mathematical puzzle" is in fact called the railway
shunting puzzle.
|
| |
| There are a number of variations,
but basically the problem which needs to be
solved is that there are two trains facing each
other on a single line with just one short siding
(which won't hold one of the two equally long
trains completely) available. In order to enable
the two trains to pass each other and continue
their journey, a string of sequential movements
using the siding is required. It's quite a
brain-teaser, which probably explains why railway
companies all over the world took the more costly
but easier way out and built passing sidings... |
|
 |
|
| |
| |
|
| |
| A question which is
often asked once the concept behind a shunting
puzzle layout has been explained is as to the
degree of complexity or, in other words: just how
many possible configurations are there? The
mathematical approach to finding out how many
permutations a specific shunting puzzle allows
for is fairly easy. If "n" is the total
number of cars on the shunting puzzle layout, and
"k" is the amount of cars which are
selected from this, then the formula to be used
is
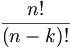
meaning that n
factorial is divided through the factorial
of n minus k (the “factorial” of
three, for example, is 1 x 2 x 3 = 6, and written
as "3!"). Applied to the original
Inglenook formula (where 5 cars are selected
froma total of 8), the calculation is as follows:
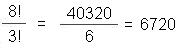
That
is to say: the 8 cars can be arranged in 40,320
different ways on the Inglenook layout, and the
number of possible trains with five cars which
can be made up from these is 6,720 (note that
this calculation only takes into account the
rolling stock present on the layout and
disregards the distribution of the three
"empty slots" in the sidings, as these
are not part of the object of the puzzle itself
and only serve as manoeuvering space; if you were
to factor them in then the number of combinations
rises significantly).
In
other words: if you were to systematically work
your way through these combinations, solving four
shunting tasks in one hour, and doing that for
three hours every evening, you would be at it for
560 operating sessions totalling 28 hours.
The true beauty of a
shunting puzzle is the simplicity within the
complexity: both Inglenook Sidings and
the Timesaver have simple rules, are
easy to understand, straightforward to build, and
great fun to operate and solve.
|
|
| |
| |
Further reading
|
| |
|
| |
| Simon Blackburn is Professor of
Pure Mathematics at the Department of Mathematics, Royal
Holloway University of London. This article looks at the
Inglenook Sidings from a mathematical perspective and
answers the question when you can be sure this can always
be done, while also addressing the problem of finding a
solution in a minimum number of moves. |
| |
| |

|
    
|
| |
Page
created: 23/SEP/2002
Last revised: 27/JUNE/2023
|